10772. Окна роз
Мистер Арнольд Геральд Ностик
занимается разработкой главного окна нового городского собора. Окно
круглое, его радиус равен 2r. Поскольку
мистер A. Г. Ностик немножко знает о девственницах, святых и ангелах, он призадумался
над геометрическим шаблоном: пусть n четное целое число, как минимум 4. Мистер
Ностик планирует выбрать n точек, каждую на расстоянии r от центра окна, так
чтобы они образовали правильный многоугольник. (На картинке приведен пример с n = 8.) Потом эти точки соединяются отрезками
и полученные области закрашиваются как показано ниже. (Цвета выбираются
произвольно.) Заметим, что при n = 8
будет всего четыре области. Пронумеруем эти области 1, 2, 3 и 4 начиная с
центральной. Всего будет n / 2
областей.
Помогите мистеру Ностику узнать,
сколько стекла каждого цвета необходимо приобрести для выкладки окна.
Вход.
Начинаются целым числом 0 ≤ m
≤ 100000; Далее следуют m строк, каждая из которых содержит r (действительное число от 1 до 100), n (четное целое от 4 до 40), и k (1 ≤ k ≤ n / 2).
Выход. Для каждой входной тройки r, n
и k в отдельной строке вывести
площадь (в квадратных единицах) k-ой
области окна, округленную до четырех десятичных знаков.
Пример входа
4
50 8 3
9.238794 8 2
10 4 1
20 4 1
Пример выхода
2928.9322
100.0000
200.0000
800.0000
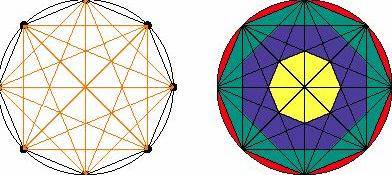
Правильный восьмиугольник Окно роз с 8 точками
в
окружности
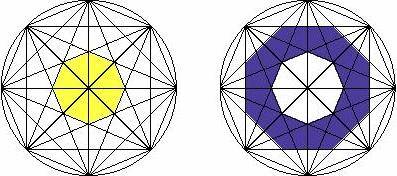
Первая область окна роз Вторая область окна роз
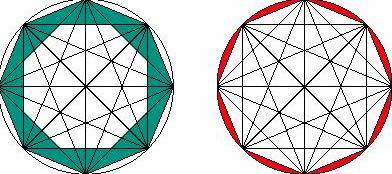
Третья область окна роз Четвертая область окна роз
РЕШЕНИЕ
геометрия
Анализ алгоритма
Покажем как найти площадь k-ой области вместе с площадями всех внутренних областей.
Такая область представляет собой правильный k-угольник.
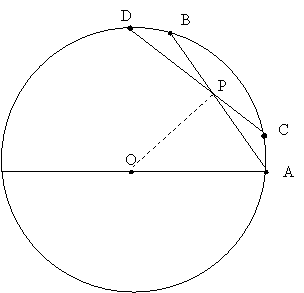
Радиусом окружности, описанной
вокруг такого k-угольника, будет отрезок OP.
Точка P образована пересечением отрезков AB и CD. При этом точки A и C, а также B и D идут
последовательно по окружности, а между A и B лежит определенное число точек. Упомянутые точки имеют координаты:
A(r, 0), ![]() ,
, ![]() ,
, ![]() .
.
Строим уравнения прямых,
проходящих через AB и CD. По правилу Крамера ищем точку их пересечения, то есть координаты точки P.
Площадь k-угольника равна n площадям равнобедренных треугольников с боковой стороной OP и углом при
вершине 2π / n. Она равна ![]() .
.
Искомую площадь k-ой области находим как разницу площадей k-угольника и (k – 1) -угольника.
Реализация алгоритма
Уравнением прямой, проходящей через точки (x1, y1) и (x2, y2), будет ax + by
+ c = 0.
void GetLine(double
x1,double y1, double
x2, double y2,
double
*a, double *b, double
*c)
{
*a = y2 - y1;
*b = -(x2 - x1);
*c = -x1*(y2 - y1) + y1*(x2 - x1);
}
Точкой пересечения прямых a1x + b1y = c1 и a2x + b2y = c2 будет P(x, y).
void GetPoint(double
a1,double b1, double
c1,
double
a2, double b2, double
c2, double *x, double
*y)
{
double d =
a1*b2 - a2*b1;
*x = (c1*b2 - c2*b1) / d;
*y = (a1*c2 - a2*c1) / d;
}
Вычисление площади k-угольника. При этом P(x, y)
и d = OP2.
double Area(double
x, double y)
{
double d =
x*x+y*y;
return
n*d*sin(2*PI/n)/2;
}
double FindSquare(int
k)
{
double
a1,b1,c1,a2,b2,c2;
double x,y;
GetLine(r,0,r*cos(2*PI*k/n),r*sin(2*PI*k/n),&a1,&b1,&c1);
GetLine(r*cos(2*PI/n),r*sin(2*PI/n),r*cos(2*PI*(k+1)/n),
r*sin(2*PI*(k+1)/n),&a2,&b2,&c2);
GetPoint(a1,b1,-c1,a2,b2,-c2,&x,&y);
return
Area(x,y);
}
Основная часть программы.
PI =
2*acos(0.0);
scanf("%d",&m);
for(i = 0; i < m; i++)
{
scanf("%lf %d
%d",&r,&n,&k);
if (k == n/2)
UpperS = PI*r*r;
else UpperS =
FindSquare(n/2-k);
DownS = FindSquare(n/2-k+1);
Res = UpperS - DownS;
printf("%.4lf\n",Res);
}